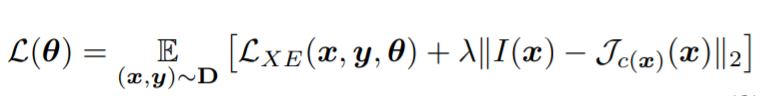ML

近期关于对抗样本Paper的综述

重新认识Adversarial Example

Posted by JohnReese on June 8, 2020

最近MIT在对抗样本领域发了一篇Paper，从观点和自己的体会来看，有点“半里程碑”的味道了。

所以以这篇Paper为基点，尝试讨论一下近期其它关于对抗样本的Paper背后的本质。

论文名是《Adversarial Examples are not Bugs, they are Features》，发表在NIPS 2019上[1]。

深度学习在图片分类领域火了好久了，但自Szegedy C等人[2]在2013年发现对抗样本后，DNN的鲁棒性这个问题也困扰相关的Researchers好久了。

刚开始的时候，我记得Ian Goodfellow认为这是由于DNN在高维空间中表现出的线性性质致使微小扰动经过DNN计算后放大致使输出产生较大的偏差。但是这样的解释总感觉有些不够，而Andrew Ilyas等人[1]就在他们的论文中尝试探讨其真正的本质。

从论文的题目中你可以直接体会到作者的观点：对抗样本不是缺陷。

尝试考虑这个过程：我们的目的是训练一个图片分类器；我们选择DNN是因为其强大的函数拟合能力；我们选择Empirical risk minimization(ERM)作为结果的衡量标准是因为我们想要准确率够高；我们为其提供庞大的数据集是因为我们想要足够泛化的结果（是泛化而不是鲁棒）；最后，DNN反馈给我们不俗的准确率。可我们不满足，我们还要求DNN表现出人类所谓的鲁棒性。但问题是，如上的过程中，我们做了哪一步致使我们可以抱有这样的预期呢？其实是因为我们先入为主了，人类默认了只能从轮胎、耳朵、外形等这些鲁棒的性质来区分狗和卡车。但说不定，是我们无知了呢？DNN发现了可以用于分类的，但我们人类无法发现的，像素层面上的feature。

Adversarial vulnerability is a direct result of sensitivity to well-generalizing features in the data.

如上，是作者对于对抗性质的一个总结——问题的根源是数据集。虽然我们不停念叨Big Data，但数据集到底需要多大才能避免DNN习得易于泛化，但其实不鲁棒的性质的问题目前应该是没有一个标准答案的。

接着来看看作者设计了怎样的实验来论证自己的观点吧：

  1. 特征函数：We define a feature to be a function mapping from the input space $X$ to real numbers, with the set of all features thus being $F = {f : X \rightarrow R}$.
  2. 在1的基础上定义 $\rho -useful$ features: For a given distribution $D$, we call a feature $\rho -useful (ρ > 0)$ if it is correlated with the true label in expectation, that is if：
  3. 鲁棒特征：

  4. 非鲁棒特征： A useful, non-robust feature is a feature which is $\rho -useful$ for some $\rho$ bounded away from zero, but is not a $\gamma-robust$ feature for any $\gamma \ge 0$.

  5. 为了便于实现，分类器比较简单：A classifier $C = (F, w, b$) is comprised of a set of features $F$, a weight vector $w$, and a scalar bias $b$:

至此，为了证明鲁棒性特征与非鲁棒性特征的存在，作者设计了四类不同的训练方式：

  1. 鲁棒数据集，标准训练方式
  2. 鲁棒数据集，对抗训练方式
  3. 非鲁棒数据集，标准训练方式
  4. 非鲁棒数据集，对抗训练方式

其中鲁棒数据集指的是由基本只含有鲁棒特征的图片组成的，即下图的

。而非鲁棒数据集基本就是人类无法依据此图片辨识出标签的，即下图的

。

那么只剩下一个问题，如何抽出鲁棒特征与非鲁棒特征从而形成两个数据集。这篇解读加上自己理解总结如下：两个数据集都是由同一个原数据集产生的。为了总结出鲁棒特征，作者首先准备了一个鲁棒的模型，然后以类似GAN的方式让准备生成的鲁棒图片和原图片在此模型的倒数第二层的输出尽可能相近（因为最后一层是线性的，也就是分类器根据d倒数第二层的特征加权得到结果）。我感觉这里不理解也没啥关系，因为你可以通过如下的训练结果直观地感受到作者的想法。

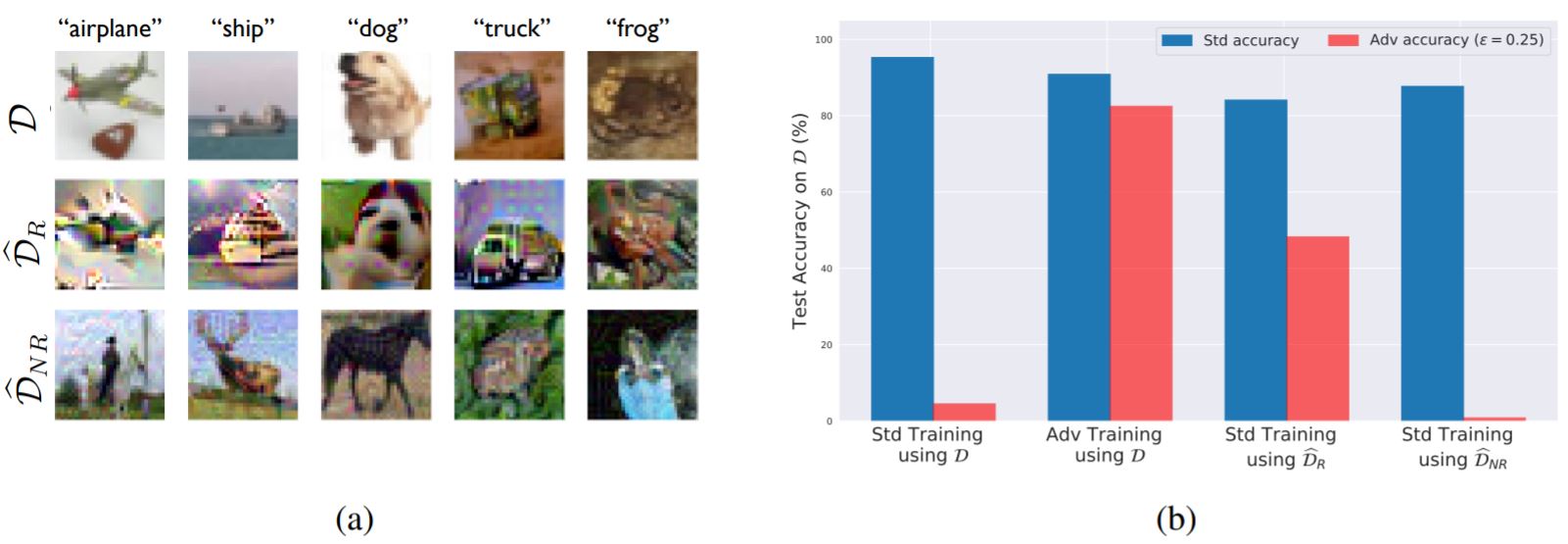
四类训练结果

这样的效果还是很有说服力的。作者为了证明这绝非偶然，准备了只有非鲁棒特征的数据集（好像是改标签的方式：标签一改肯定习得不出来人类所认为的鲁棒特征）来训练DNN，发现在测试集的表现上足够好。这就证明像素层面的feature同样是有一定的泛化性的。

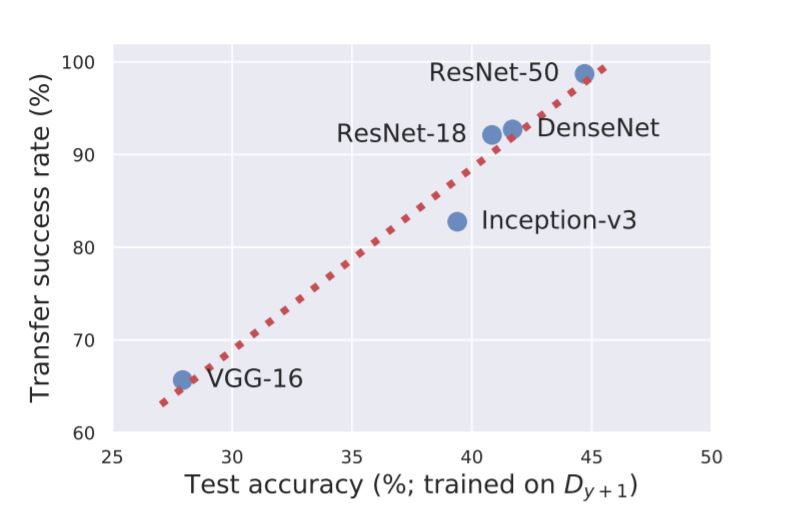
另外，作者从这个论点出发，尝试解释了对抗样本的可转移性：如果一个网络架构的准确率越高，就越有可能习得非鲁棒的feature（见下图）。

四类训练结果

那么，从这个本质出发，我觉得提升鲁棒性无非就是在传统的训练过程中的每个环节花一点额外的心思：

数据集

[3]也是最近的一篇文章，提出了高斯补丁的方法。

四类训练结果

从上图中可以很直观地理解实现方式（$W$控制补丁大小，$\sigma$控制扰动大小）。其实加噪声的方法通过以上的论述可以很好地解释为在不经意间“毁坏”了像素层面的feature致使DNN去寻找其它feature从而提升了鲁棒性。

训练方法

[4]是发表在NIPS 2019上的文章。虽然只有两位作者，但我觉得质量很高。

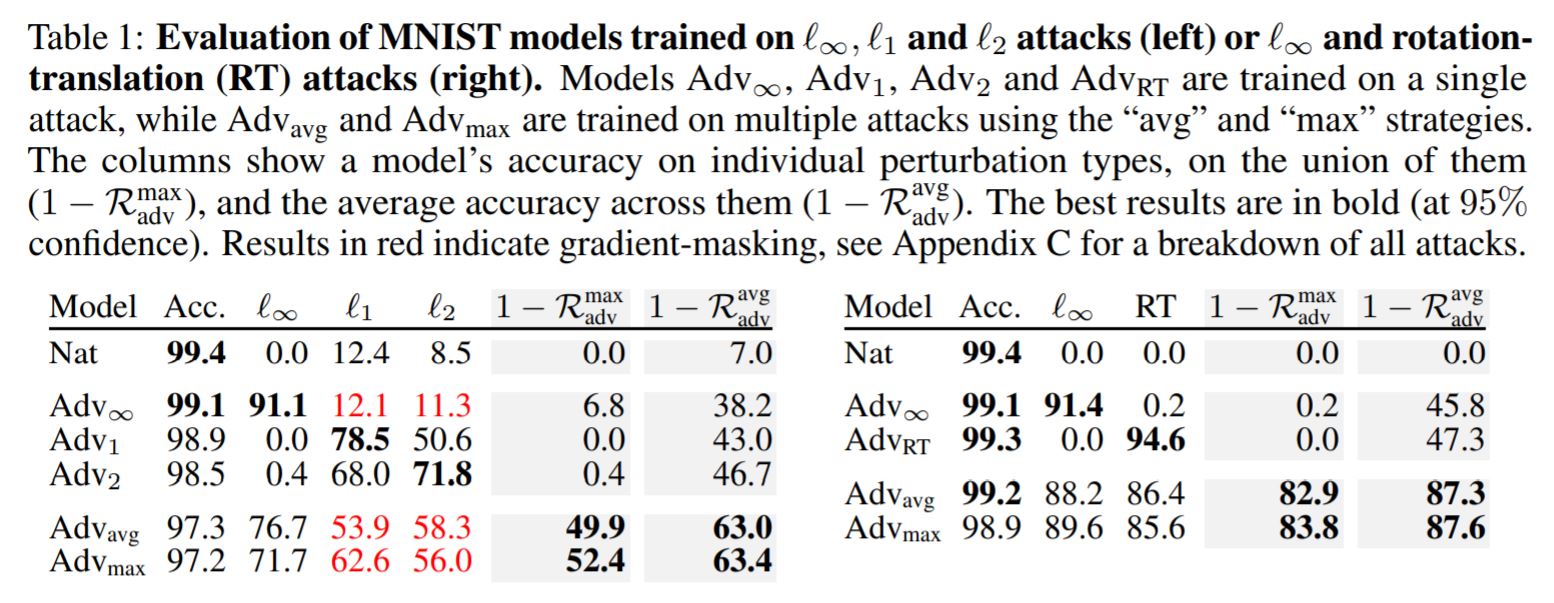
作者在其中提出了目前鲁棒性训练存在的一个问题：鲁棒性训练方法往往只对一种攻击方式有效（这里解释下攻击方式有哪些：1范数，2范数，无穷范数，旋转以及缩放等）。并且作者枚举且“证明”了一些互相排斥的扰动（证明看不懂）：

  1. Small $l_{\infty}$ 和 $l_1$ Perturbations are Mutually Exclusive
  2. Small $l_{\infty}$ and Spatial Perturbations are (nearly) Mutually Exclusive

因此，作者提出一种新的训练方式(其实有些显然>-<):

其中对于$S$的解释：

We assume $n$ perturbation types, each characterized by a set $S$ of allowed perturbations for an input $x$. The set $S$ can be an $l_p$-ball or capture other perceptually small transforms such as image rotations and translations. For a perturbation $r \in S$, an adversarial example is $\hat{x} = x + r$(this is pixel-wise addition for $l_p$ perturbations, but can be a more complex operation, e.g., for rotations).

实验结果是很棒的：虽然每一项的抗扰动值都低于最优的一种训练方法，但其它方面都是遥遥领先，做到了“全面鲁棒”。

多扰动训练结果

那么，对于以上的多扰动问题我也尝试YY一下：可能在像素层面上有不少的非鲁棒性feature，而只针对单一范数进行训练并不能保证DNN会迁移到鲁棒特征上，可能还有其它范数层面上的非鲁棒性feature。

[5]尝试将可解释性与鲁棒性联系在一起，其训练目标如下：

可解释训练方法

其中的$I(x)$是预先计算的关于雅可比矩阵的函数。没看懂，我蒙一下：$I(x)$映射到输入层对应的是鲁棒特征所在的像素部分，比如耳朵，尾巴等；而最右边的雅可比矩阵是当前训练所得到的，它应该和$I(x)$越近越好，这样子就表明当前的导数更新是由可解释的像素部分所决定的。但是好像实验结果并不是很惊艳。

以上都是2019年左右的论文，比较新。但[4]和[5]都引用了一篇MIT在2017的Paper，其引用数有点咂舌，同时也有干货，所以也放到一起讲讲[6]。

这篇文章探讨的内容也非常有深度，作者尝试将鲁棒性训练的目标归结为如下的式子：

其中$S$的定义和[4]中差不多。

Our perspective stems from viewing the saddle point problem as the composition of an inner maximization problem and an outer minimization problem.

同时从以上这段话了解到，上式称为鞍点问题，拆解开来就是两部分：内部的最大化问题和外部的最小化问题。作者认为目前的攻击方法其实就是求解内部最大化问题；而鲁棒性训练方法就是求解外部最小化问题。

作者提到虽然成功求解上式意味着DNN完全从理论上达到了鲁棒，但这涉及到：

tackling both a non-convex outer minimization problem and a non-concave inner maximization problem.

即处理一个非凸的外部最小化问题和一个非凹的内部最大化问题。作者的贡献就是展示了在一定程度上解决上述问题是可控的。

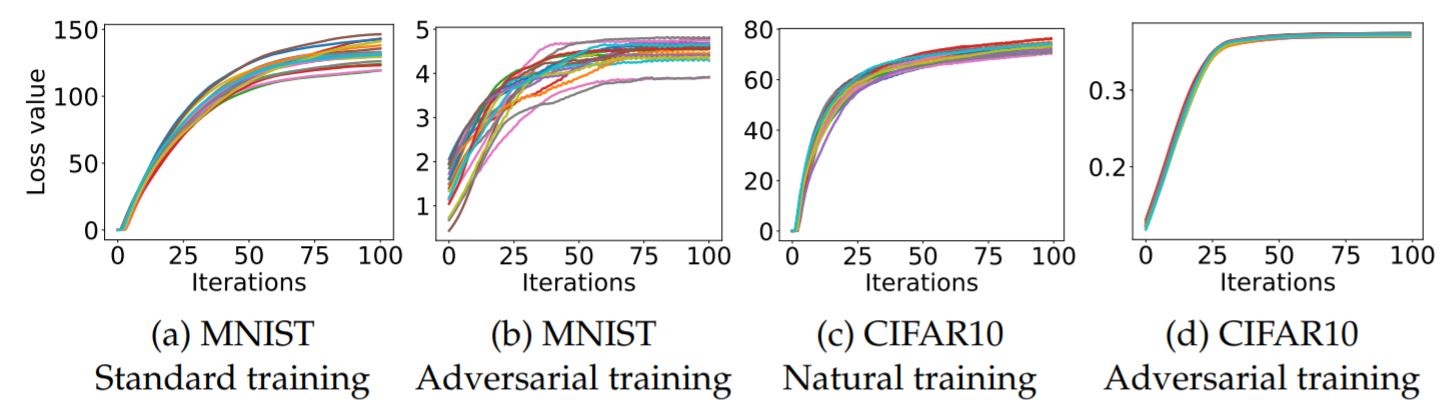
首先讨论内部最大化问题，先上图：

相近的损失函数值

你是不是觉得太不专业了，画在一起根本看不清嘛。但这恰恰证明了作者的观点：作者跑了很多次很多次的实验，发现最终的损失函数是相近的。也就是说，我们虽然无法求解其最优解，但是我们却能以大概率保证发现的次优解其实和最优解差不多。

这里有一点需要提及，作者是通过Fast Gradient Sign Method (FGSM):

的多次迭代版本projected gradient descent(PGD):

来最大化内部值的（那个不是连乘符号，可以参看此博客，是投影符号。功能类似截断，避免产生过于极端的对抗样本）。而且作者发现能够对于PGD攻击鲁棒就意味着对于所有一阶攻击鲁棒。

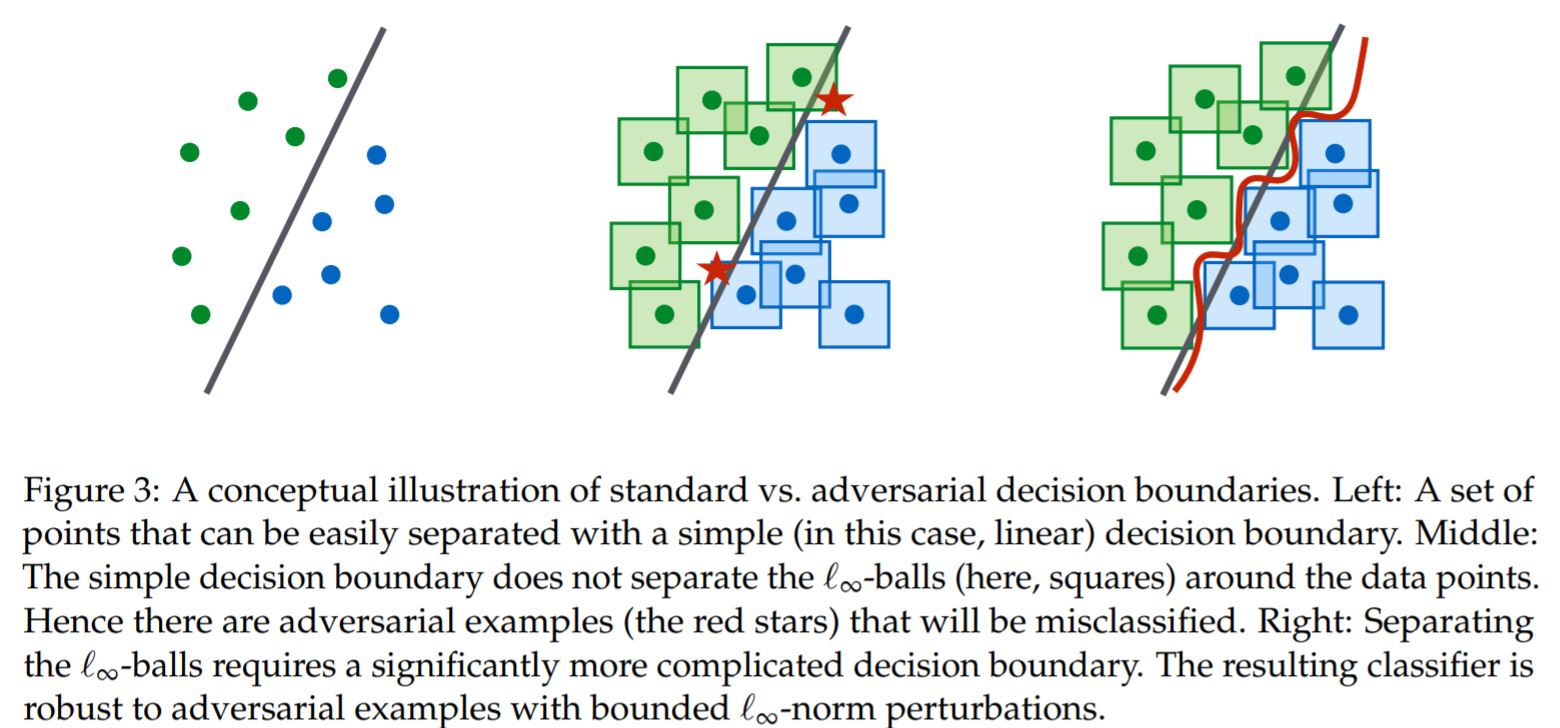
综上，PGD基本解决内部最大化问题。接着，如何最小化外部值。先上图：

决策边界

不想看英文的话就是普通训练方法只会习得线性决策边界。其中方块代表对圆点样本产生微小扰动后的可能样本范围，所以两颗星星就代表由于过于简单的决策边界而被误分类的样本。而预期边界应该是右图。所以通过以上猜想我们有理由认为DNN的表达能力，即capicity对于鲁棒性很重要。

作者针对MNIST做了相关实验，其中因为对细节不是完全清楚就不放上来误人子弟了，就把作者自己归纳的结论翻译一下：

  1. 在仅使用自然样本(除了增加精确性之外)进行训练时，增加网络的容量可以增加对一步扰动的鲁棒性。
  2. 在小容量网络的情况下，试图针对强大的对手(PGD)进行训练会阻止网络学习任何有意义的内容。该网络始终收敛于预测一个固定的类，即使它可以通过标准训练收敛到一个准确的分类器。
  3. 鞍点问题的值随着容量的增加而下降，说明该模型对对抗实例的拟合效果越来越好。

其实以上结论用一句话概括就是鲁棒性很难学，因此对于DNN的capicity要求很高。

以上就是本文的大致内容，进一步的探讨就不展开了。

  1. Ilyas A, Santurkar S, Tsipras D, et al. Adversarial examples are not bugs, they are features[C]//Advances in Neural Information Processing Systems. 2019: 125-136.
  2. Szegedy C, Zaremba W, Sutskever I, et al. Intriguing properties of neural networks[J]. arXiv preprint arXiv:1312.6199, 2013.
  3. Lopes R G, Yin D, Poole B, et al. Improving robustness without sacrificing accuracy with patch gaussian augmentation[J]. arXiv preprint arXiv:1906.02611, 2019.
  4. Tramèr F, Boneh D. Adversarial training and robustness for multiple perturbations[C]//Advances in Neural Information Processing Systems. 2019: 5858-5868.
  5. Noack A, Ahern I, Dou D, et al. Does Interpretability of Neural Networks Imply Adversarial Robustness?[J]. arXiv preprint arXiv:1912.03430, 2019.
  6. Madry A, Makelov A, Schmidt L, et al. Towards deep learning models resistant to adversarial attacks[J]. arXiv preprint arXiv:1706.06083, 2017.
FEATURED TAGS
生活 Jekyll ML Algorithm RL 形式化 Java