项目总结
这个链接https://www.bilibili.com/video/av81034357/是上传的程序演示视频。
1. 项目背景(需求分析)
随着计算机的发展,各类工业系统广泛应用在各行各业,验证这些系统的正确性尤为重要,特别是一些关键领域如航天航空、轨道交通等,一旦出现错误可能造成非常严重的后果。模型检测是一种很重要的自动验证技术,它可以自动执行,并能在系统不满足性质时提供反例路径,因此在工业界非常受推崇。
关于线性时态逻辑公式(Linear Temporal Logic, LTL)转换成等价自动机(通常是Bϋchi自动机)的研究已经进行了将近三十年。这种转换是基于自动机的模型检验的关键。Gerth等人在《Simple on-the-fly automatic verifaction and Flavio Lerda》提出了一种将LTL公式转化为Bϋchi自动机的on-the-fly构造方法,即使只构造了部分属性自动机,也可以检测反例。
在《On the Relationship between LTL Normal Forms and Bϋchi Automata》一文中,作者提出了一种新的构造Bϋchi自动机的方法,利用了析取范式(disjuctive-normal forms,DNF)。对于任意LTL公式φ都有等价的DNF范式$\bigvee_i(\alpha_i \land X \varphi_i)$,其中$\alpha_i$是有限字的合取,且$\varphi_i$是LTL公式的合取。在文中提到,任意LTL公式都可以转换成等价的DNF范式,且$\bigvee_i(\alpha_i \land X \varphi_i)$可以用$\phi$来表示。任意LTL公式都可以构造标签迁移系统(labelled transition system,LTS)。
LTS是构造自动机的第一步.特别地,对于Until/Release-Free的LTL的公式,可以给LTS添加一组接收状态直接获得Bϋchi自动机。构造Bϋchi自动机最难的部分是确定是确定可接收状态集合。
本文利用析取范式,对于Until/Release-Free的LTL的公式,然后转换成与LTL公式等价的Bϋchi自动机。故本项目即为对其理论的具体实现。
2. 概要设计
2.1 基本概念
-
LTL公式的NNF形式:否定符号只出现在原子命题前面的LTL公式,且具有如下形式:
- DNF形式:当一个公式可以用$\bigvee_i(\alpha_i \land X \varphi_i)$表示,这个公式就是析取范式(DNF),$\alpha_i$是有限的文字合取,并且$\bigvee_i(\alpha_i \land X \varphi_i)$也是一个文字,或者是一个Until,Next,或者Release公式。
-
LTS转移系统:DNF公式λ对应的LTS转移系统定义如下:
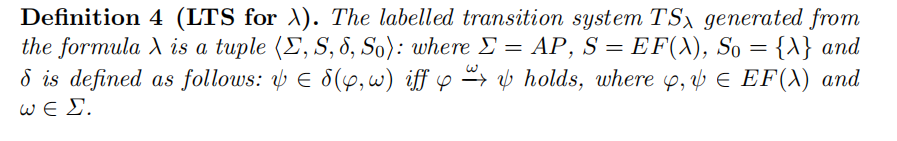
2.2 把LTL公式转成DNF公式
对于一个NNF LTL公式$\varphi$,我们使用论文中的引理1,递归地产生$\varphi$对应的DNF公式DNF($\varphi$):
递归完成后,我们就会得到NNF LTL公式$\varphi$对应的集合形式的DNF公式,集合里面的元素就是$\varphi := \bigvee_i(\alpha_i \land X \varphi_i)$里面的$(\alpha_i \land X \varphi_i)$.
另外,在这一步中,我们求出DNF($\varphi$)中每个$(\alpha_i \land X \varphi_i)$里面的$\varphi_i$对应的DNF($\varphi_i$),并且对所有的$\varphi_i$也进行这个操作,直到所有的DNF形式都是之前求出来过的为止,这一步是为了方便后面自动机转移关系的求解。
2.3 求出DNF公式对应的LTS
我们根据转移系统LTS的定义来求出DNF($\varphi$)对应的转移系统LTS:
$\Sigma = 2^{AP}$ :原子命题集合,其中AP包含了原子命题和原子命题的否定,这也是为什么我们原子命题的否定的原因,在这样的定义下,原子命题和它的否定是没有区别的。
$S = EF(\varphi)$ :状态集合,其中EF($\varphi)$)是$\varphi)$加上前面循环求出的所有的DNF公式中每个$(\alpha_i \land X \varphi_i)$里面的$\varphi$的集合,并不只是DNF($\varphi)$)中每个$(\alpha_i \land X \varphi_i)$里面的$\varphi$的集合,还包括了DNF($\varphi$)及之后重复这个过程所求出的$\varphi$的集合。
$S = {\varphi}$ :初始状态集合,里面只包括$\varphi$
$\delta(\varphi, \omega)$:转移关系,这是最关键的一步,对于每个状态来说,以$\varphi$为例, DNF($\varphi$)中每个$(\alpha_i \land X \varphi_i)$,我们有$\delta(\varphi, \alpha_i) = \varphi_i$,对每个状态都是这样求出它的所有转移关系。在这一步,对每个状态,我们都要根据它的DNF公式来求解转移关系,这就是2.2节我们求出所有DNF公式的原因。
2.4 求解LTS对应的自动机
由定义5可知,LTL公式$\varphi$对应的自动机就是在LTS的基础上添加终止状态集合F得到的,若$\varphi$是Release-free公式(即$\varphi$中不出现R的公式),则其终止状态集合$F={True}$;若$\varphi$是Until-free公式(即$\varphi$中不出现U的公式),则其终止状态集合$F=S$,即所有的状态集合。
至此,整个求解LTL公式$\varphi$对应的自动机的过程结束。
3. 约定
为了便于程序的输入输出,我们对于LTL的符号进行确认或改写。
- Next : X
- Release : R
- Until : U
- /\ : A
- \/ : O
- atomic proposition: a~z
- parentheses : ), (
- True: T
- False: F
其中,论文中所考虑的是LTL公式的NNF形式,即所有的否定都会被压缩到literal level。因此,本项目不考虑否定符号。
另外,G,即Always也在论文提及可用Release等价替换,就不在此赘述。
4. 思路分析
-
拆分LTL公式
如上图的引理所示,首先根据六条规则将LTL公式化为DNF的形式。显然需要在代码中使用递归的想法。
-
建立有向边(转移)
假设$\varphi=(a \land b \land X(\psi))$,则从$\varphi$通过
ab指向$\psi$。以此类推建立从$\varphi$出发的边。 -
循环操作
另外,如果$\psi$是没有出现过的子公式,则需要进一步对其进行直至没有新的子公式出现。
-
建立终止状态
根据论文4.2的定义,分别根据公式为
Until-Free还是Release-Free分别设定不同的终止状态。
5. 具体实现
-
算法最为关键的核心就是LTL公式的拆分,核心思路是使用递归实现,源代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90
def convertToDNF(subformula, level): """ @description: convert the LTL formula to the DNF form @param: subformula{str}: LTL formula. level{int}: recurrent Level. @return: dict: each object indicates the CNF clause. """ # Termination if len(subformula) == 1: if subformula == 'F': # special case for False return [] return packageFormula(subformula, 'T') elif subformula[0] == 'X': # process the CNF in X() subformula = subformula[2:-1] posList = [] pos = 0 cnt = 0 for t in subformula: if t == '(': cnt += 1 elif t == ')': cnt -= 1 elif t == 'O' and cnt == 0: posList.append(pos) pos += 1 if len(posList) == 0: return packageFormula('T', subformula[1:]) else: posList.append(len(subformula)) tempList = [] st = 0 for ed in posList: tempFormula = subformula[st:ed] tempList += packageFormula('T', tempFormula) st = ed + 1 print("CNF occurs in the X:", tempList) return tempList left = 'left' operater = 'operater' right = 'right' rightIndex = 0 # Process if subformula[0] != '(': if subformula[0].islower() or subformula[0] == 'T' or subformula[0] == 'F': left = subformula[0] operater = subformula[1] rightIndex = 2 elif subformula[0] == '(': # (|left(1:pos)|) # 0| |pos match = 1 pos = 1 for t in subformula[1:]: if t == ')': match -= 1 if match == 0: break elif t == '(': match += 1 pos += 1 left = subformula[1:pos] operater = subformula[pos+1] rightIndex = pos + 2 else: print('Sth unexpected happened near Process!') # extract the right part if subformula[rightIndex] == '(': right = subformula[rightIndex+1:-1] else: right = subformula[rightIndex:] # choose the different action based on the operator if operater == 'A': ... return formulaList elif operater == 'R': t1 = convertToDNF('('+left+')A('+right+')', level+1) t2 = convertToDNF('('+right+')A(X('+subformula+'))', level+1) t3 = t1 + t2 elif operater == 'U': ... elif operater == 'O': ...
可以看到
Termination注释下就是递归的返回条件:要么此时子公式已经被分解到原子命题的程度;要么就是X形式。其中对于X形式我们还特别处理了其中可能存在的DNF形式。因为根据论文的内容X形式中不能含DNF形式。同时
left,operator和right三部分分别代表着LTL公式一般可以左部分,操作符和右部分。将其记录就可以带入下一层的递归计算。最后U和O的代码段与R段类似,故以省略号替代。
- 第二关键的就是如何建立Buchi自动机,或者说有向图。代码实现如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
q = Queue() q.put(testFormula) while not q.empty(): currentFormula = q.get() listOfDNF = convertToDNF(currentFormula, 0) print(listOfDNF) cleanFormula(listOfDNF) print(listOfDNF) for ele in listOfDNF: newFormula = formulaToStr(ele['xFormula']) print("new Formula:", newFormula) if mapDict.get(newFormula, -1) == -1: q.put(newFormula) updateMap(newFormula) nodes.append(newFormula) newAtomic = atomicToStr(ele['atomic']) print("new Atomic", newAtomic) edges.append({'u': currentFormula, 'v': newFormula, 'label': newAtomic})
可以比较直观地看出来就是常用的使用队列建立图的方法。其中我们需要判断生成的子公式是否原来出现过,否则会导致代码产生死循环。
-
主要数据结构解析
我们主要使用
python中的dictionary数据类型保存LTL公式的每个clause。假设当前$\varphi = (a \land b \land X(c)) \lor …$。则其对应的dict对象为:
1
[{'atomic': ['a', 'b'], 'xFormula': ['c']}, ...]
最外层使用
list进行包裹,方便程序实现合并操作。
6. 算法时间复杂度分析
整体算法分为2步:拆分LTL公式;建立Buchi自动机。但是这两步是在一个整体的循环中。具体可以参考如下的伪代码。
1
2
3
4
5
6
while 队列不为空
取出新的子公式a
拆分a
if 有新的子公式:
则插入队列
从a建立有向边
显然整体的时间复杂度是while循环次数乘以内部的运算次数。
根据论文的结论我们可得,对于Until/Release-Free的LTL公式最多有$2^{n+1}$个状态,其中$n$为子公式的个数,所以while的循环次数是$O(2^{n+1})$。
另外相较于建立有向边,拆分公式的复杂度忽略不计。而建立有向边的次数与状态数相关,因此总体的时间复杂度为$O(2^{2(n+1)}), 其中n为子公式的个数.$
7. 测试
鉴于LTL的递归拆解异常复杂,我们的每个Test Case都是经过手动推导,再与程序生成的进行比较。所以虽然整体的数量不多,但是保证准确。所以可以用我们的Test Case来测试其它程序,相信我们程序的准确率是比较高的。
另外由于绘图库的功能限制,初始状态我们以st:开头,终止状态我们以绿色表示。
-
$X(aOb)$: 这是一个特别关键的例子。因为根据论文里的描述
X中不能够出现$\lor$的DNF形式。所以不可能出现aOb出现在状态中。虽然它的正确性是显然的。.png)
-
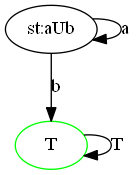
$aUb$: 为论文里的例子,正确性不再赘述。
-
$a \land b \land c$: 即
aAbAc,同样因为是一步的状态,正确性也是显然的。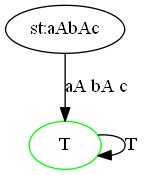
-
$Ga$: 即
FRa,证明如下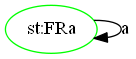
-
$(Xa)Ub$: 令$\varphi=(Xa)Ub$,证明如下
Ub.png)
-
$X(aUb)$: 证明如下:
.png)
-
$(aUb)\land (cUd)$: 因为没有$X/R/U$,所以正确性比较显然。
A(cUd).png)
-
$aR(Xb)$: 证明如图所示
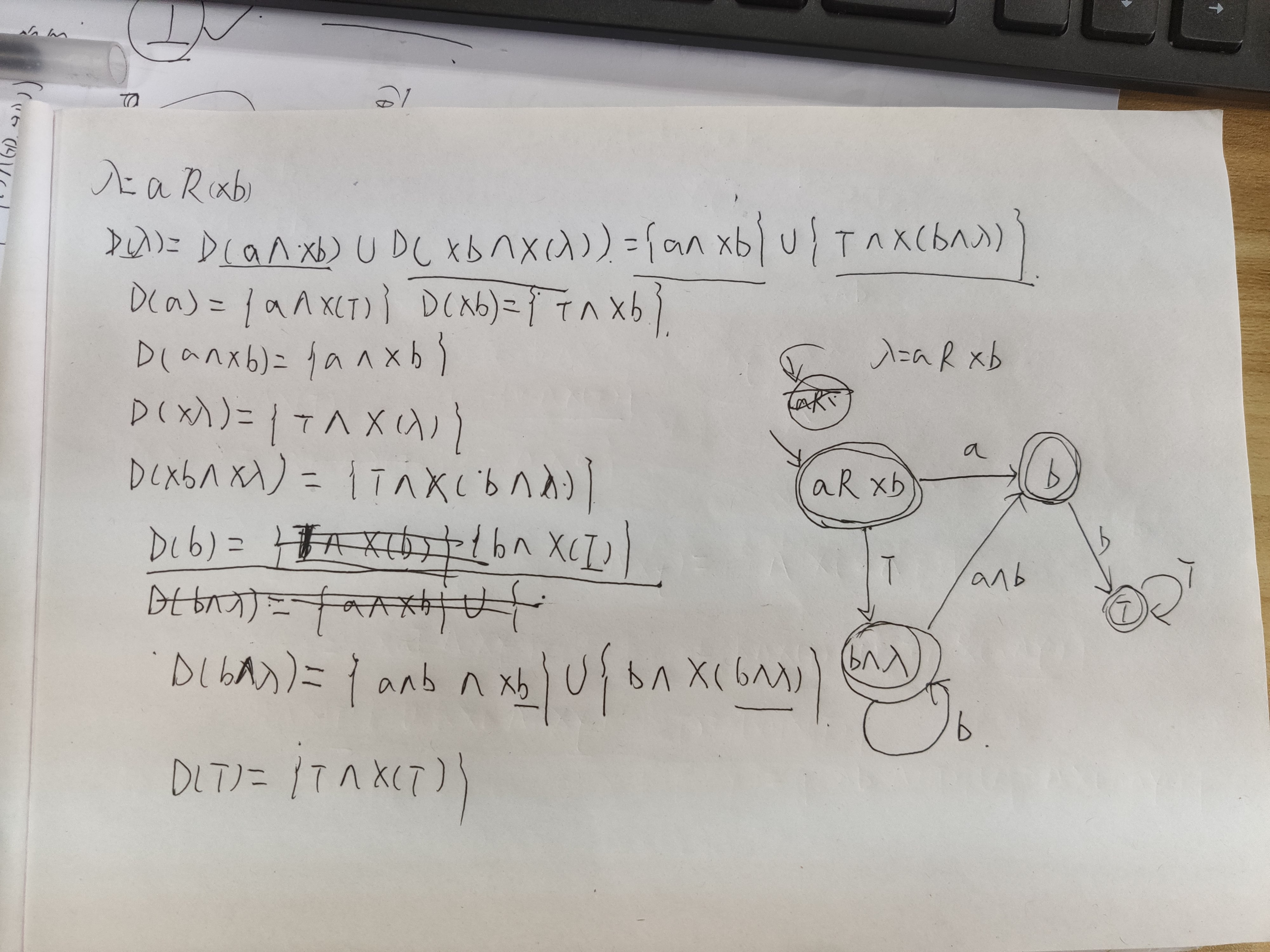
.png)
