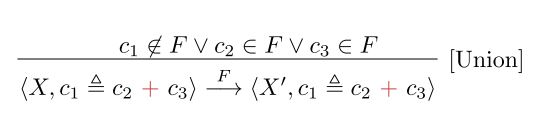Background

Maude

1. Rewrite: op and rl.
2. Search: search and Model-Checker.

Clock Constraint Specification Language(CCSL)

1. Clock: tick idle tick idle …(infinite).
2. Constraint: Clock A must tick after Clock B tick.
3. Scheduling: decide each clock when to tick.

But

When we search the key words(Maude and CCSL) in Google. To our surprise, there is one paper which have implemented it.

Soooo! Creation => Reproduction

Implemention

Final Results

Github: https://github.com/Callmejp/CCSL2Maude

Some Statistics:

Comprehension To CCSL

1. Formal Definition:
   • definition:
   $$Clock: (c_n)_{n \in N^+}.\\ Clock Sets: C = \{c_1, c_2, ..., c_n\}.\\ Schedule: \delta: N^+ \rightarrow 2^C.\\ History: \chi: C \times N^+ \rightarrow N.$$
   • example:
   $$C = \{c_1, c_2\}.\\ c_1 = tick, tick.\\ c_2 = idle, tick.\\ \delta(1) = \{c_1\}, \delta(2) = \{c_1, c_2\}.\\ \chi(c_1, 1) = 1, \chi(c_1, 2) = 2.\\ \chi(c_2, 1) = 0, \chi(c_2, 2) = 1.\\$$

2. Constraints:

   

Generate the expected CCSL sequence

1. Key Code Segment:

   1
   2
   3
   4
   5
   6
   7
   crl [next] : < (F, F') ; PHI ; X ; K > => < (F, F'); PHI ; update(X, F) ; K + 1 >
     if F =/= empty /\ satisfy(F, X, PHI) .
      
   ***(
     F is the subset of Clocks that will tick at the time step (K + 1) .
     And the precondition is the schedule will satisfy all constraints(i.e. PHI).
   )
   

According to our understanding, we think the formalization of a clock system doesn’t express the if and only if(i.e. $\Leftrightarrow$).

For example, as the figure below shows: if there is a constraint $c_1 \triangleq c_2 + c_3$, then condition $c1 \notin F \lor c_2 \in F \lor c_3 \subset F$ can satisfy it.

But, it’s clear that $c_1 \in \delta(n) \Leftrightarrow c_2 \in \delta(n) \land c_3 \in \delta(n)$ express the ` bidirectional relationship`.

So, state $c_1 \notin \delta(n) \land c_2 \in \delta(n) \land c_3 \notin \delta(n)$ apparently satisfy the formalization of a clock system, but it can’t satisfy the original defination of Union Constraint.

As a result, we abstract the constraints based on the original definitions and our understanding.

1
2
3
  --- Union 
  eq satisfy(F, ([C1, TL1, N1], [C2, TL2, N2], [C3, TL3, N3], X), C1 != C2 + C3) = 
    if (C1 in F) then ((C2 in F) or (C3 in F)) else (not ((C2 in F) or (C3 in F))) fi .

Moreover, you can check all test cases in the TestCaseForConstraints.md included in the github repository.

Periodic scheduling

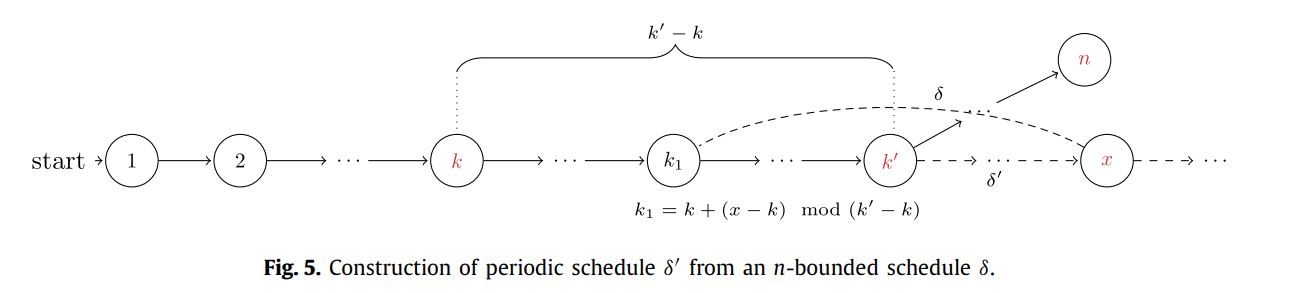
There is a paradox between the finite sequence we can generated and the formal verication to the infinite sequence.

So, as the figure below shows, periodic scheduling can solve the problem to some extent.

In short, all clocks have the same cycle.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
eq isPeriodic(([C1, TL1, N1],[C2, TL2, N2], X), (C1 < C2) PHI, K, K') = 
  tick(TL1,K) == tick(TL1,K') and
  tick(TL2,K) == tick(TL2,K') and
  sd(N1,num(TL1,K)) >= sd(N2,num(TL2,K)) and
  isPeriodic(X,PHI,K,K') .

***(
    C*: Clock's name
    TL*: Tick-List(tick, idle, ...)
    N*: Nat
    PHI: Constraints
    K: start of the cycle
    K': end of the cycle
)

We think the code above written in the paper has a logical error. As you can see, isPeriodic(X,PHI,K,K') will remove the C1 & C2 in the X. But if there’re other constraints that include C1 & C2, it will apprently cause errors when running programs.

1
2
3
4
5
eq isPeriodic(([C1, TL1, N1], [C2, TL2, N2], X), (C1 < C2) PHI, K, K') = 
    get(TL1, K) == get(TL1, K') and
    get(TL2, K) == get(TL2, K') and
    sd(N1, cal(TL1, K)) >= sd(N2, cal(TL2, K)) and
    isPeriodic(([C1, TL1, N1], [C2, TL2, N2], X), PHI, K, K') .

You can also check our implemention and test cases in our repository.

Formal verification by (bounded) model checking

The content is mainly about the detection of Deadlock via search in Maude and LTL verification via Model-checker in Maude.

We have to admire the authors’ profound understanding and application of Maude. As you can see in the code segment, bounded and periodic schedule can both happen at the same time.

1
2
3
4
5
6
7
8
9
10
11
crl [next] : < (F, F') ; PHI ; X ; K > => < (F, F'); PHI ; X' ; K + 1 >
    if F =/= empty /\
	   satisfy(F, X, PHI) /\
	   X' := update(X, F) /\
	   getPeriod(X', PHI, K, K + 1) == 0 .

crl [periodic] : < (F, F') ; PHI ; X ; K > => < (F, F') ; PHI ; rollback(X', P) ; sd(K + 1, P) >
    if F =/= empty /\
	   satisfy(F, X, PHI) /\
	   X' := update(X, F) /\
	   P := getPeriod(X', PHI, K, K + 1) .

By the way, rollback is done by ourselves.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
  --- Code Segment in fmod ConFIGURATION
  var X : Conf .
  vars K N1 : Nat .
  var Y : ConfElt .
  var C1 : Clock .
  var TL1 : TickList .
  
  op rb : ConfElt Nat -> ConfElt .
  eq rb([C1, TL1, N1], 0) = [C1, TL1, N1] .
  eq rb([C1, (TL1, 1), N1], K) = rb([C1, TL1, N1 - 1], K - 1) .
  eq rb([C1, (TL1, 0), N1], K) = rb([C1, TL1, N1], K - 1) .

  op rollback : Conf Nat -> Conf .
  eq rollback(empty, K) = empty .
  eq rollback((Y, X), K) = rb(Y, K), rollback(X, K) . 

Generate specific sequences

It’s clear that there may be many Schedules satisfing the Constraints. Take a step further, maybe user have their preferences based on requirements. For example, try to generate the Schedule that tick as little as possible, or as much as possible.

Authors defined these requirements as Policy.

Practical implemention are based on the META-LEVEL in Maude.

Main idea is generating all the schdule and pick the schdule satisfing the Policy.

Example: Laziness: to specify a set of lazy clocks that only tick if they have to tick at each step.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
--- all for getNonTickConf (WDNMD)
  eq getLastIdle(([C1, TL1, N], X), C1) = lastIsIdle(TL1) .
  
  eq existNonTick(empty, C) = false .
  eq existNonTick((X | CF), C) = if getLastIdle(X, C) then true else existNonTick(CF, C) fi .
  
  eq pick(empty, C) = empty .
  eq pick((X | CF), C) = if getLastIdle(X, C) then X | pick(CF, C) else pick(CF, C) fi .

  eq getNonTickConf(CF, C) = if existNonTick(CF, C) then pick(CF, C) else CF fi .

  --- rules
  crl [next] : [ < F ; PHI ; X ; K >, P ] => [ < F ; PHI ; X' ; K + 1 >, P ]
    if X' := getConfByPol(getAllSuccessors(< F ; PHI ; X ; K >, 0), P) .

  ceq getAllSuccessors(< F ; PHI ; X ; K >, N) = downTerm(T, nil) | getAllSuccessors(< F ; PHI ; X ; K >, N + 1) 
    if RT := metaSearch(upModule('MAIN, false), upTerm(< F ; PHI ; X ; K >), '<_;_;_;_>[upTerm(F), upTerm(PHI), 'X':Conf, upTerm(M + 1)], nil, '+, 1, N) /\ ('X':Conf <- T) := getSubstitution(RT) .

  eq getConfByPol(CF, lazy(empty)) = CF .
  eq getConfByPol(CF, lazy(C | CS)) = getConfByPol(getNonTickConf(CF, C), lazy(CS)) .

For a variety of reasons, this part is difficult for us. As you can see, just for implementing the function getNonTickConf, we write other 3-4 functions.

Concluding remarks

1. Maude: FrameWork for Formal Verification.

2. CCSL: Like the SAT problem to some extent.

   $$Union \Rightarrow (c_1 \rightarrow c_2 \lor c_3) \land (c_2 \lor c_3 \rightarrow c_1)\\ \Rightarrow (\lnot c_1 \lor c_2 \lor c_3) \land (\lnot(c_2 \lor c_3) \lor c_1)$$

• ← Previous Post
• Next Post →